SA approach
Calculation steps
The following diagram illustrates the calculations:
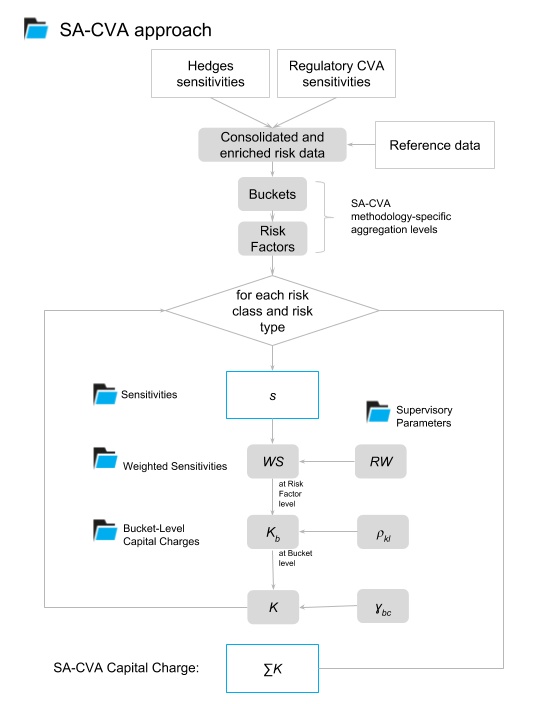
Here is a high-level description of the algorithm:
- Read and process sensitivities - $s$.
- Assign methodology specific:
- Regulatory Risk Factor;
- Regulatory Bucket;
- to each input sensitivity record.
- For each asset class and risk type:
- Calculate Weighted Sensitivities -$WS$:
- obtain Risk Weights - $RW$ - for each input sensitivity record;
- multiply sensitivity by Risk Weight.
- Calculate Bucket-Level Capital Charges - $K_b$:
- aggregate Weighted Sensitivities along SA-CVA Risk Factors;
- obtain Correlations for pairs of Risk Factors inside each Bucket - $\rho_{kl}$;
- use the variance-covariance formula to aggregate risk factor level Weighted Sensitivities into Bucket-Level Capital Charges.
- Calculate Capital Charge - $K$:
- obtain Cross-Bucket Correlations - $\gamma_{bc}$
- use the variance-covariance formula to aggregate Bucket-Level Capital Charges
- Calculate Weighted Sensitivities -$WS$:
- Obtain total SA-CVA Capital Charge - $ΣK$- by summing Capital Charges across risk classes and risk types.
Reading and processing sensitivities
The Solution expects to receive from the upstream risk/cva engine and data management systems:
- sensitivities of the Regulatory CVA. See also Transaction Level CVA Sensitivities.
- sensitivities of hedges,
- meta-data to allocate sensitivities to regulatory buckets/risk factors.
Transaction Level CVA Sensitivities
If the upstream risk system can attribute netting set level sensitivities down to transactions driving CVA, then the optional attribute “NettingSetTradeId” could be used to provide trade identifiers. In this case it is possible to decompose sensitivity inputs down to trades in the user interface.
For the what-if analysis feature it is recommended to recompute sensitivities for an affected netting set and override/delete previously supplied sensitivities. Alternatively, an incremental impact of new trades can be provided in addition to previously supplied sensitivities.
Sensitivities processing
Once sensitivities are retrieved from the sensitivities file, these steps are required:
- enrich sensitivities with CreditQuality, Sector, Size, Region and other fields for classification into regulatory buckets - see Reference Data section;
- allocate the sensitivities to regulatory vertices:
- this step is required only if the provided tenors do not match the ones required by the regulation - see also Regridding.
Bucket and risk factor
This section describes Buckets and Risk Factors which are specific aggregation levels defined by the methodology, they are most probably different from the definition of buckets and risk factors for internal risk management.
Regulatory Risk Factors
Paragraphs [MAR50.54] - [50.77] specify a certain definition of risk factors (subscript ~k~ in the methodology).
Risk factors are further used:
- as a parameter for defining Risk Factors Correlations,
- as an aggregation level for weighted sensitivities (see the variance-covariance formula in [MAR50.52] for Bucket-Level Capital Charges).
The resolved Regulatory Risk Factors can be transparently displayed using this hierarchy: [RegulatoryRiskFactor].[RegulatoryRiskFactor].
This table is summarizing the combinations of fields used to assign risk factors for Delta and Vega. In most of the cases, risk factor definitions are based on the buckets, which are described in the next section.
| Risk Class | Delta Risk Factor definition | Vega Risk Factor Definition |
|---|---|---|
| Interest Rate | [CurveType].[CurveType], [RiskFactorCcy].[RiskFactorCcy], [Vertices].[Vertices]1 | [CurveType].[CurveType], [RiskFactorCcy].[RiskFactorCcy] |
| Foreign Exchange | [RegulatoryBucket].[RegulatoryBucket] | [RegulatoryBucket].[RegulatoryBucket] |
| Counterparty Credit Spread | [ReferenceName].[ReferenceName], [Vertices].[Vertices] | - |
| Reference Credit Spread | [RegulatoryBucket].[RegulatoryBucket] | [RegulatoryBucket].[RegulatoryBucket] |
| Equity | [RegulatoryBucket].[RegulatoryBucket] | [RegulatoryBucket].[RegulatoryBucket] |
| Commodity | [RegulatoryBucket].[RegulatoryBucket] | [RegulatoryBucket].[RegulatoryBucket] |
Regulatory Buckets
For each risk class and sensitivity type, paragraphs [MAR50.54] - [50.77] specify the way sensitivities are grouped into Buckets - $b$.
Buckets are further used:
- as a parameter for defining Risk Weight,
- as an aggregation level for Bucket-Level Capital Charge.
The resolved Regulatory Buckets can be transparently displayed using this hierarchy: [RegulatoryBucket].[RegulatoryBucket].
Whenever possible ActiveViam will provide a generic algorithm or reference data to apply bucketing. Clients may also provide their own bucketing logic and reference data in their input files.
A waterfall approach is applied:
- If the RegulatoryBucket has been provided in the input file, it has a priority.
- If the RegulatoryBucket has not been provided, the Bucket is derived by ActiveViam based on the buckets configuration files.
Buckets configuration files contain mappings of the sensitivity fields to the SA-CVA Buckets. Their content needs to be updated to fit organization’s data. The next table summarizes combinations of fields for the buckets lookup.
| Risk Class | Buckets lookup fields (both Delta and Vega) |
|---|---|
| Interest Rate | [RiskFactorCcy].[RiskFactorCcy] |
| Foreign Exchange | [RiskFactorCcy].[RiskFactorCcy] |
| Counterparty Credit Spread | [Sector].[Sectors] |
| Reference Credit Spread | [Sector].[Sectors], [CreditQuality].[CreditQuality] |
| Equity | [Size].[Size],[Economy].[Economy], [Sector].[Sectors] |
| Commodity | [CommodityGroup].[CommodityGroup] |
Weighted Sensitivities
Weighted sensitivities are computed for each input sensitivity record.
Risk Weights
Paragraphs [MAR50.54] - [50.77] specify the rules for assigning Risk Weights $RW$ to sensitivities.
Risk Weights lookup is defined per Risk Class and Sensitivity type. It is either based on a lookup of combination of fields or a constant value.
| Risk Class | RW for Delta | RW for Vega |
|---|---|---|
| Interest Rate | single value for not-liquid/not-domestic currencies or inflation. Set of values per tenor otherwise. | single value |
| Foreign Exchange | single value | single value |
| Counterparty Credit Spread | specified per Bucket and Credit quality | single value |
| Reference Credit Spread | specified per Bucket | single value |
| Equity | specified per Bucket | specified per Bucket |
| Commodity | specified per Bucket | single value |
Formula for the Weighted Sensitivities
Once the risk weights, $RW$, are assigned, the weighted sensitivities $WS$ are computed according to:
$$WS = s \cdot RW$$
The formula in [MAR50.50] contains a subscript $k$ referring to the risk factor level of aggregation.
Bucket-Level Capital Charge
Weighted sensitivities netted at Risk Factor level are rolled up into Bucket Level Capital Charges $K_{b}$ using a variance-covariance type formula – see [MAR50.52].
Risk Factors Correlation
Pairs of risk factors need to be assigned a cross-risk factor correlation $\rho_{kl}$.
The important consideration is, that since correlations are used to obtain bucket level capital, they are defined only for the pairs of Risk Factors that belong to the same SA-CVA bucket.
Interest Rate
For the Vega risk factors, correlations are defined as a single value. For the Delta risk factors, definition is based on these cases:
| Case | Correlation |
|---|---|
| One of the risk factors is inflation | single value |
| Risk factors for a liquid or domestic currency | depends on the pair of tenors |
| Risk factors for other currencies | single value |
Counterparty Credit Spread
Applicable only to Delta risk factors, since Vegas are not calculated.
Inside a SA-CVA Bucket, there might be Risk Factors that belong to the same or different credit entities, credit quality and tenors. The definition depends on the properties of the credit name and tenors:
| Same | Legally related | Same Credit Quality | Same Tenor | Correlation |
|---|---|---|---|---|
| Y | 0,9 | |||
| N | Y | Y | 0,9 | |
| N | Y | N | 0,81 | |
| N | N | Y | Y | 0,5 |
| N | N | Y | N | 0,45 |
| N | N | N | Y | 0,4 |
| N | N | N | N | 0,36 |
Since regulatory risk factors are defined as buckets for risk classes:
- Foreign Exchange,
- Reference Credit Spread,
- Equity,
- Commodity
There will be only one risk factor in each bucket and correlations are not defined.
Formula for the Bucket-Level Capital Charge
Risk factor level Weighted Sensitivities $WS_k$, together with Risk Factors Correlations $rho_{kl}$ are variables in the bucket-level capital charge formula, defined in [MAR50.52]:
The disallowance parameter, R, is one of the Supervisory parameters and set at 0.01 in [MAR50.52].
SA-CVA Capital Charge
Bucket level capital charges are rolled up into risk class/sensitivity type level capital charges using a variance-covariance type formula [MAR50.53] and then aggregated across risk classes/sensitivity types.
Cross-Buckets Correlation
For the next aggregation step, we need to obtain cross-bucket correlations - denoted as $\gamma_{bc}$ in [MAR50].
Here is how it is defined for each Risk Class:
| Risk Class | Delta and Vega |
|---|---|
| Interest Rate | single value |
| Exchange Rate | single value |
| Counterparty Credit Spread (Delta only) | depends on the pair of buckets |
| Reference Credit Spread | depends on the pair of buckets |
| Equity | depends on the pair of buckets |
| Commodity | depends on the pair of buckets |
Formula for the SA-CVA Capital Charge
Obtaining the final SA-CVA Capital Charge is a two-step calculation:
-
For each risk type and sensitivity type, bucket level capital charges are aggregated according to [MAR50.53]:
$$K = m_{\text{CVA}} \cdot \sqrt{\sum_{b}^{}K_{b}^{2} + \sum_{b}^{}{\sum_{c \neq b}^{}\gamma_{\text{bc}} \cdot K_{b} \cdot K_{c}}}$$where $K_{b}$ is Bucket-level Capital Charge, $\gamma_{bc}$ is Cross-bucket Correlation and $m_{CVA}$ is a supervisory parameter - CVA multiplier - set at 1.0 in [MAR50.41].
-
The total SA-CVA Capital Charge is calculated as a simple sum of the aggregated charges from step 1 across sensitivity types (delta and vega) and risk classes.
Specifically, when CurveType is “Inflation” then Risk Factor is defined as CurveType plus RiskFactorCurrency, else when RiskFactorCurrency is liquid or domestic - then Risk Factor is defined as CurveType plus RiskFactorCurrency plus Tenor, else - CurveType plus RiskFactorCurrency (similar to Inflation risk).
In case input sensitivities are based on more granular risk factors than required by regulation