BA approach
Calculation steps
The following diagram illustrates the BA calculations.
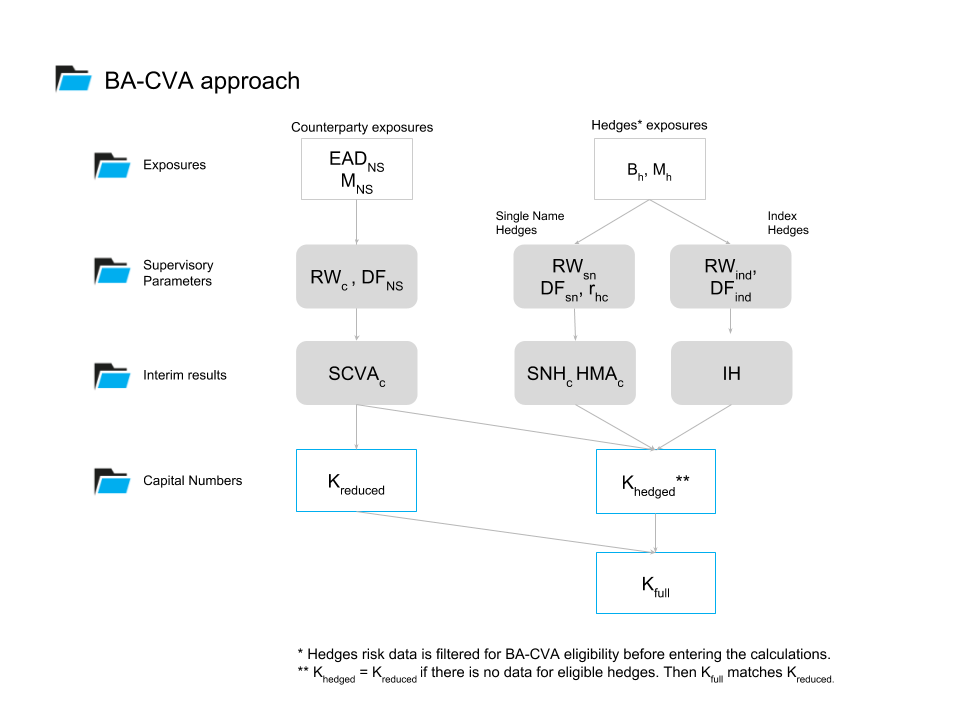
Logical steps of the BA-CVA calculation:
- Read and process input data:
- EADs, Hedge Notionals and Maturities;
- Reference data - trades, netting sets, counterparties and reference instruments. For more details, please refer to the Reference Data section.
- Assign supervisory multipliers:
- obtain Risk Weights - $RW$ - for each of the input records;
- compute supervisory Discount Factors - $DF$ - for each of the input records;
- define hedge-counterparty correlations - $r_{hc}$ - for single name hedges.
- Compute interim results
- Stand-alone CVA Capital - $CVA_{c}$ - for each counterparty;
- Single-name Hedge Parameter - ${SNH}_{c}$ - for each counterparty;
- Index Hedge Parameter - $IH$ - for the CVA portfolio;
- Calculate Hedge Misalignment parameter - $HMA_{c}$ - for each counterparty.
- Compute capital numbers:
- Hedged BA-CVA Capital - $K_{hedged}$ - by aggregating the interim numbers;
- Reduced BA-CVA Capital - $K_{reduced}$ - by filtering out hedges risk data;
- BA-CVA Capital Charge - $K_{full}$ - by weighting the reduced and hedged capital measures.
Reading and processing risk data
Clients implementing BA-CVA approach need to provide information about credit exposures (exposures at default, effective maturities) and eligible hedges (notionals, remaining maturities). For the detailed specification of the fields please refer to Input Data File Formats.
The input data can be transparently displayed using measures in the “Exposures” folder.
The minimum data set (Reduced BA-CVA)
The Reduced version of BA-CVA calculation requires only the exposures at default $EAD_{NS}$ and effective maturities $M_{NS}$ of the netting sets.
Eligible hedges risk data (Full BA-CVA)
Eligible hedges risk data (notionals $B_{h}$ and remaining maturities $M_{h}$ reduces BA-CVA capital charge under the Full BA-CVA approach.
The Solution expects that eligibility of hedges according to [MAR50.10] is evaluated by the upstream data management/risk system.
BA-CVA calculation requires static attributes, e.g. sector, credit quality and region, for the credit names - both for counterparties and hedge reference credit instruments - we assume they can be retrieved from the input data files described in the Reference Data section.
If eligible hedges risk data is not provided, hedging parameters described in Section “Full version of the BA-CVA (hedges are recognised)” do not provide any capital relief, and Full BA-CVA calculations produce the same results as the Reduced BA-CVA approach.
Supervisory parameters
The measures, such as risk weights, discount factors, hedge-counterparty correlations, are available in folder “Supervisory parameters” in BA section.
Risk Weights
Netting sets and hedge trades risk data is enriched with Risk Weights:
-
For the credit exposures and single name hedges, risk weights $RW_{NS}$ and $RW_h$ are selected based on sector and credit quality of the netting set counterparty or hedge reference name.
-
For the Index hedges, risk weights $RW_i$ require information about the index members and their weights (see IndexMembers and MemberWeights in the Reference names attributes). Once the risk weights of individual members are defined based on their sector and credit quality, an average of individual risk weights is multiplied by 0.7.
where $m$ is member of index $i$, $w_{m}$ - is the weight of member $m$ in index $i$ such that $\sum_{m}w_{m} = 1$ , $RW_{m}$ - is the risk weight of member $m$.
Discount Factors
BA-CVA approach uses the following formula to compute supervisory discount factor for each netting set or hedge trade:
-
$DF\ = \ 1$- if the provided ${EAD}_{NS}$ has been computed using IMM approach (see hierarchy [TradePosition].[UnderIMM] and
-
$DF = \frac{1 - \ e^{- 0.05 \cdot M}}{0.05 \cdot M}$ - otherwise.
In the above formula $M$ is the effective maturity of the netting set or the remaining maturity of the hedge trade.
Hedge-Counterparty Correlation
The impact of single-name hedges depends on how closely the hedge’s reference credit name is correlated with the CVA counterparty it is intended to hedge. Hedge-Counterparty correlation is defined for each single name eligible hedge trade.
The correlation - $r_{\text{hc}}$ - is obtained by comparing the hedge’s reference name and the counterparty’s static data and depends on these cases:
| Case | $$r_{\text{hc}}$$ |
|---|---|
| They are the same | 100% |
| They are legally related1 | 80% |
| They are in the same sector and region | 50% |
If a reference name and a counterparty do not fall into any of the cases above, then the correlation is zero and the hedge trade doesn’t contribute into reduction of capital (that should not happen due to the definition of eligible hedges - please see [MAR50.19]). Hedging with instruments, not referring a counterparty directly - increases the Hedging Misalignment Parameter, which is described below.
Interim results
Individual components of the capital formulae are available for analysis and validation via the measures in folder “Interim measures”.
Stand-alone CVA Capital
Now the weighted and discounted netting set level exposures can be aggregated up into counterparty level Stand-alone CVA Capital according to the formula (this is a slightly rearranged formula from [MAR50.15] - constants are put inside the summation):
where $\alpha$ is set at 1.4.
Stand-alone CVA Capital at Counterparty level is aggregated into portfolio-level capital measures - see sections Reduced BA-CVA Capital and Hedged BA-CVA Capital.
Single-name Hedge Parameter
Single-name Hedge Parameter offsets stand-alone capitals in the Full BA-CVA approach.
The Single-name Hedge Parameter is denoted as $SNH_{c}$ in [MAR50] - and aggregates the notionals of single-name hedge trades (hedge instruments risk data where IsSingleName is true) according to the formula in [MAR50.23] (superscript ^SN^ was omitted for simplicity here):
where $r_{hc}$ is supervisory hedge-counterparty correlation, described above.
Hedging Misalignment Parameter
When hedging with instruments, not referring the counterparty directly, capital relief from hedges is partially offset with the Hedging Misalignment Parameter $\text{HMA}_{c}$ defined in [MAR50.25]:
Index Hedge Parameter
The very last hedging “parameter” is the Index Hedge Parameter, which is denoted as $IH$ in [MAR50]. It is computed for all index hedge trades - i - in the portfolio (IsSingleName is false) according to the formula set in [MAR50.24]:
BA-CVA Capital Charge
Finally, capital charges are evaluated (see folder Capital):
-
K_full - is the primary result of the BA-CVA approach. It combines the Reduced BA-CVA Capital and Hedged BA-CVA Capital using the weights set out in [MAR50.20].
-
K_reduced- is computed from the netting sets risk data only, hedges are not recognized.
-
K_hedged- is the core result of the Full BA-CVA method.
Reduced BA-CVA Capital
Stand-alone CVA Capital on counterparty level can be rolled up to the portfolio level according to the formula set in [MAR50.14], the resulting measure is Reduced BA-CVA Capital:
where $\rho$ is the supervisory counterparty correlation parameter set at 0.5.
Hedged BA-CVA Capital
Single-name Hedge and Hedging Misalignment parameters together with the Index Hedge parameter are aggregated into the Hedge BA-CVA Capital according to [MAR50.21]:
Components of the formula, in particular:
Systematic components of CVA risk:
Idiosyncratic components of CVA risk:
Hedge Misalignment Parameter:
SCVA net of SNH:
are present in the cube as measures for analytical purposes (see folder “Interim measures”).
BA-CVA Capital Charge
Full BA-CVA Capital measure weights the results of the Reduced BA-CVA Capital and Hedged BA-CVA Capital as follows:
where $\beta$ is set at 0.25.
Full BA-CVA and missing hedges risk data
When the Solution does not receive eligible hedges risk data, the hedging parameters provide zero contribution to the Hedged BA-CVA capital formula (SNH=0, IH=0, HMA=0).
Full BA-CVA measures are still computed, however they provide the same results as the Reduced BA-CVA:
-
See “Legal relationship” input data file in the Reference data section. ↩︎