Market Risk Accelerator Reference Guide v2.0.0VaR Interpolation
The percentile is a well-defined concept in the continuous case, but there are multiple ways to compute it from a discrete sample.
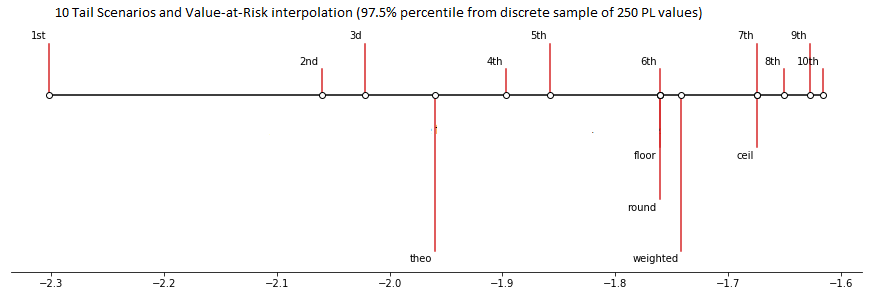
Consider the following example. This is a plot of the 10 smallest values in a sample of 250 values drawn from the standard normal distribution. The plot shows the theoretical 2.5% quantile of the standard normal distribution (“theo”) as well as various types of 97.5 percentile estimation (floor, ceil, weighted, etc).
The MRA Accelerator supports multiple types of VaR estimation, as described in this chapter.
Calculation steps
The algorithm can be described as follows:
- Compute quantile as (1-confidence level)
- Compute adjacent ranks based on Quantile2Rank setting, quantile and discrete sample size
- Sort PL and obtain PL values for the adjacent ranks
approximate VaR from the PL values using the interpolation formula controlled by the
rounding.varproperty
Computing adjacent ranks
The property “rounding.quantile2Rank” can be used to control the rank calculation:
| Property value | Description | Formula for rank | Example | Notes |
|---|---|---|---|---|
| rounding.quantile2Rank =CENTERED | This corresponds to the “First variant, C=1/2” of the interpolation variants described on this wiki | x = quantile * vectorSize + 0.5 | (1-97.5%) x 250 + 0.5 = 6.75 | |
| rounding.quantile2Rank =EQUAL_WEIGHT | This corresponds to the “Third varian, C=0” of the interpolation variants described on this wiki | x = quantile * (vectorSize+1) | (1-97.5%)x (250+1) = 6.275 | default option |
| rounding.quantile2Rank =EXCLUSIVE | x = quantile * (vectorSize+1)-1 | (1-97.5%)x (250+1)-1 = 5.275 |
Based on the computed x, we can obtain various adjacent ranks:
- x_lower = round_down(x)
- x_higher = round_up(x)
- x_nearest = round(x)
- x_nearest_even = round_to_even(x)
- weight = x mod 1
VaR approximation
The property rouding.var can be used to control the interpolation.
| Property value | Description | Formula for VaR | Notes |
|---|---|---|---|
| rouding.var =FLOOR | Simulated PL for the lower of the adjacent ranks | VaR = PL_lower | |
| rounding.var =CEIL | Simulated PL for the higher of the adjacent ranks | VaR = PL_higher | default option |
| rouding.var=WEIGHTED | Simulated PL linearly interpolated between the adjacent ranks | VaR = weight * PL_lower + (1-weight) * PL_higher | |
| rouding.var =ROUND | Simulated PL for the nearest rank VaR = PL_nearest | ||
| rouding.var=ROUND_EVEN | Simulated PL for the nearest even rank | VaR = PL_nearest_even |
where PL values are defined as follows (in the sorted PL vector):
- PL_lower as x_lower smallest value
- PL_higher as x_higher smallest value
- PL_nearest as x_nearest smallest value
- PL_nearest_even as x_nearest_even smallest value